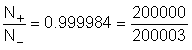Die Eigenschaften des Spinensembles

Das NMR-Phänomen kann, wie in der Herleitung modellhaft beschrieben, am Einzelkern, sozusagen im mikroskopischen Maßstab, erklärt werden. NMR-Spektroskopie, das Messen realer Proben, lässt sich jedoch nur auf makroskopischer Ebene durch Betrachtung vieler Einzelspins (Spingruppen, Spinensembles) interpretieren.

Platziert man eine Gruppe von Spins mit I = ½ im Magnetfeld H₀, so kann sich jeder Spin in zwei Richtungen orientieren, die man häufig als +½ und -½ oder als α und β bezeichnet.

Das Resonanzexperiment (siehe Beziehung für ΔE ) besteht nun darin, Spins vom tieferen Energieniveau in das höhere anzuregen und die absorbierte Energie über die zugehörige Frequenz zu messen bzw. die Frequenzemission der Spins bei der Rückkehr in den Grundzustand zu detektieren.

Leider befinden sich nicht alle Spins vor der Anregung im Grundzustand, was für die Intensität des Resonanzsignals sehr günstig wäre, sondern es gilt für deren Verteilung auf Grundzustand (N_-) und angeregten Zustand (N₊) die Boltzmann-Statistik :

N+, N- Besetzungszahlen im Grundzustand (-) und im angeregten Zustand (+) ΔE Energieunterschied der beiden Zustände k Boltzmannkonstante (= 1.3805·10-23 J/K) T absolute Temperatur

Sehen Sie sich dazu bitte auch ein interaktives Beispiel an.

Von ca. 400000 Spins befinden sich somit nur 3 mehr im Grundzustand, und nur die können angeregt werden! Das NMR-Experiment lebt also von einer sehr kleinen Populationsdifferenz, die man im Verlauf der Messung behutsam behandeln muss. Verliert man durch zu starke Energiezufuhr diesen minimalen Überschuß im Grundzustand, so gibt es nichts mehr anzuregen und in der Folge kann kein Resonanzsignal detektiert werden (Sättigung des Spinsystems).

Es muss daher nach der Anregung des Spinsystems darauf geachtet werden, dass vor einem neuerlichen Resonanzexperiment ausreichend lange gewartet wird, um durch Rückkehr der auf β gehobenen Spins in den Grundzustand wieder das Boltzmanngleichgewicht zu erreichen. Das dafür nötige Intervall wird als Relaxationszeit T₁ bzw. longitudinale Relaxation oder Spin/Gitter-Relaxation bezeichnet

Im H₀-Feld platzierte Spinpakete bzw. –ensembles (z. B. vom gleichen Proton in einem Molekül stammend) lassen sich am einfachsten durch einen von den Spins generierten Magnetisierungsvektor beschreiben, dessen Größe für das betrachtete Atom proportional zu (N_- - N₊) ist.

Die Vektorsumme der Magnetisierungsvektoren aller Spinpakete eines Moleküles (d.h. aller von den verschiedenen Atomen durch unterschiedliche chemische Verschiebung generierte Magnetisierungen) bezeichnet man als Netto-Magnetisierung oder Überschußmagnetisierung M_z.

Entsprechend der Festlegung für das NMR-Koordinatensysten ist dieser Überschußmagnetisierungvektor M_z im Zustand des Boltzmanngleichgewichtes gemeinsam mit dem H₀-Feld in Richtung der z-Achse orientiert.

Vom magnetischen Moment μ des Einzelspins zur Überschußmagnetisierung M_z des Moleküls (Spinensemble)

M_z setzt sich also aus der Summe aller Verschiebungsbeiträge der Atome eines Moleküls zusammen und enthält die gesamte Frequenzinformation, die letztlich nach Anregung des Spinsystems (z. B. mittels eines Hochfrequenzpulses) durch Fouriertransformation zum NMR-Spektrum führt.

Für die Wahl der Messparameter eines NMR-Experimentes ist es auch wichtig, die Empfindlichkeit des zu messenden Isotops zu kennen. Eine Auflistung für in der Praxis der Strukturaufklärung wichtige NMR-Kerne ist in der folgenden Tabelle gegeben.

Die relativen Empfindlichkeiten werden hauptsächlich durch die natürliche Isotopenhäufigkeit, die Boltzmannverteilung und das magnetische Moment (in welches auch das gyromagnetische Verhältnis einfließt) bestimmt.

Kerne mit I = ½ sind bezüglich ihrer Resonanzfrequenzen und NMR-Spektren einfacher interpretierbar, da sie mit –½ und +½ nur Grund- und angeregten Zustand aufweisen, höherzahlige Spins weisen wesentlich komplexere Besetzungsschemata auf. Angenehmerweise besitzen die wichtigen NMR-Kerne wie ¹H, ¹³C, ¹⁵N, ¹⁹F, ²⁹Si und ³¹P einen Spin von I = ½