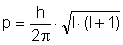Quantelung des Kernspins

Es lässt sich quantenmechanisch auf Basis der Schrödinger- Gleichung zeigen, dass nur gewisse Werte für den Kernspin p erlaubt sind, dieser daher "gequantelt" ist:

h Planck'sches Wirkungsquantum I Kernspinquantenzahl p Kernspin

Die Quantelung des Kernspins p und somit des magnetischen Moments μ (siehe Gleichung für das magnetische Moment) erfolgt über die Kernspinquantenzahl I. Verschiedene Isotope sind durch unterschiedliche Spinquantenzahlen charakterisiert.

Der Wert von I ist abhängig von der Protonen- und Neutronenanzahl eines Atomkernes und resultiert – vereinfacht dargestellt – aus einer Vektorsumme von Einzelspinbeiträgen der Kernbausteine. Wegen der teilweisen Kompensation dieser Spinbeiträge durch bspw. Spinpaarung kann der Zahlenwert nicht absolut und direkt aus der Protonen/Neutronenanzahl abgeleitet werden.

Es gilt jedoch allgemein:

• I kann halbzahlig sein
• I kann ganzzahlig sein
• I kann Null sein

Die Halb- oder Ganzzahligkeit der Kernspinquantenzahl I (nicht aber der absolute Zahlenwert!) kann jedoch aus der Gerad- bzw. Ungeradzahligkeit der Protonen und Neutronenanzahl und aus den daraus resultierenden Masse- und Ordnungszahlen für ein Isotop abgeleitet werden:

Ableitungsregeln für die Größe der Kernspinquantenzahl

Im interaktiven Periodensystem können Sie Daten zu allen NMR aktiven Kernen finden.

Kerne mit I = 0 (bspw. das Kohlenstoffisotop ¹²C) können sofort für alle weiteren NMR-Betrachtungen ausgeschlossen werden, da aus der Beziehung des Magnetischen Moments und der Resonanzbedingung ersichtlich ist, dass ohne magnetisches Moment μ keine Resonanz auftreten kann.

Folglich wird das magnetische Moment μ durch die Kernspinquantenzahl I bestimmt:

γ gyromagnetisches Verhältnis

Das bedeutet, dass das magnetische Moment ebenso "gequantelt" ist, also sich nicht kontinuierlich, sondern nur in „erlaubte" Richtungen orientieren darf.