Logarithmic-potential Theory

Author: Edmund A. Laport

Logarithmic potentials have been mentioned frequently in the previous chapters of this book and have been used to obtain essential design information for antennas and transmission lines. The logarithmic-potential method of calculating various antenna and transmission-line parameters is an invaluable tool for the antenna engineer. With it, he can calculate quickly, and with sufficient accuracy, problems that would otherwise cost him enormous amounts of time and labor.

All students of electrophysics are familiar with logarithmic-potential theory, but as customarily taught it is associated entirely with electrostatic theory. By the straight electrostatic method, the computations for engineering usage are unnecessarily complicated. In engineering one may take advantage of certain well-known dynamic relationships which, at a certain point in the work, lead to valuable direct approaches to the desired answers. In the method to be described,¹ electrostatic principles are used only for writing the potential equations due to the charges on a system of cylindrical conductors that are parallel to a perfectly conducting plane called the "ground" or "image" plane. After the potential equations have been written and condensed to a compact form, use is made immediately of the dynamic concept of the characteristic impedance of a transmission line expressed in terms of its capacitance per unit length and the velocity of propagation of transverse electromagnetic waves in the system. From then on, in one step one has found the formula for the capacitance per unit length of the system and in the next step the characteristic-impedance formula.

Another dynamic relationship that is employed directly is that which exists between the charge and current. This relationship is as follows: The current I flowing in a wire is related to the charge per unit length Q on the wire by

Therefore in any system where v is constant, the current is directly proportional to the charge per unit length. This permits one to interpret charge ratios directly as current ratios.

The meter-kilogram-second system of units and common logarithms are used, which accounts for the numerical coefficients that appear in all equations. The charge per unit length Q is in coulombs per meter on each conductor, identified by subscript for the conductor of that number and by double subscript for its image charge, which is always of the opposite sign of the charge on the conductor. In order to apply to each logarithmic term the sign of the real or image charge under consideration, reciprocal distances are used for all linear distances from the axes of the conductors. This avoids the problem of signs, because the sign of the logarithm of a reciprocal of a distance will then always be the same as that of the charge from which this distance is measured - otherwise, it would always have the opposite sign. Furthermore, we shall take advantage of the fact that a transmission line of low loss, which includes almost all practical radio-frequency lines, has a characteristic impedance Z₀ = , and since v = 1/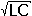, Z₀ = 1/vC. The velocity of propagation v for air-dielectric systems has the value 3·10⁸ meters per second. The capacitance per unit length is defined in the usual way as the charge per unit length divided by the potential difference, Q/V.

All cross-sectional dimensions must be in the same units (inches or centimeters), and the ground is assumed to be perfectly conducting.

1)	Due to Brown