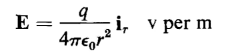Capacitance of Concentric Spheres

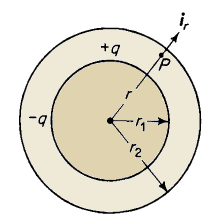Figure 2-11. Concentric spheres.

Suppose that a charge of +q coulombs is uniformly distributed over the surface of a sphere having a radius r₁. Also, this sphere is concentric with a sphere of larger radius r₂, which carries a charge of -q coulombs, as shown in Fig. 2-11. Consider a point P in the space between spheres at a distance r from the common center. The electric field intensity at P due to the charge +q on the surface of the inner sphere is according to Eq. 2-5

[2-26]

The electric field intensity due to the charge -q on the inner surface of the outer sphere is zero in accordance with Gauss's theorem.

The field within the two concentric spheres then is taken completely into account by considering only the positive or negative charge, as the case may be, on the inner sphere. Then the electric field intensity at a point between the spheres at a distance r from the center is

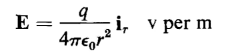
and the difference of potential between the two concentric spheres is

[2-27]

The capacitance between spheres is

[2-28]

Example 2-1:

Figure 2-12(a) shows the sketch of a cell for making measurements of dissipation factor and dielectric constant of liquid dielectrics. The plates of the cell are two concentric spherical sections mounted and spaced from each other on a conical Pyrex glass plug. The conical plug has a generating angle of 30°. The liquid dielectric occupies the space between the spherical sections, i.e., between the radii r2 and r1. Within the glass plug is a gold foil guard electrode having the same radius of curvature as the inner sphere, namely r1 but insulated by a very small gap from the inner sphere. The purpose of the guard electrode is to prevent fringing; it is so connected that the capacitive and leakage current to it by-pass the measuring circuit. Such cells are used in a-c bridge circuits. When the bridge is balanced the guard circuit is at the same potential as the inner sphere. 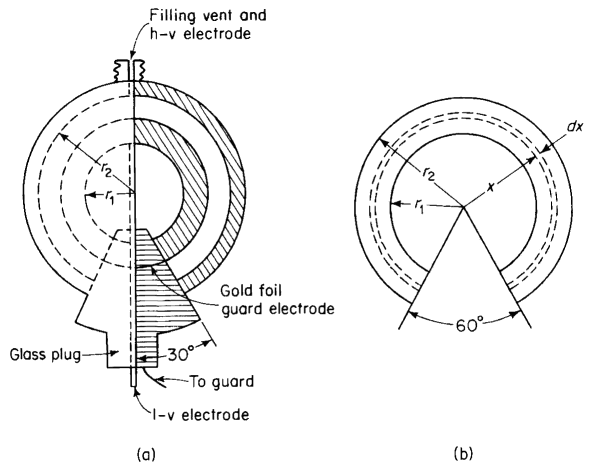Figure 2-12. (a) Dielectric test cell; (b) elemental shell in test cell The inside radius r2 of the outer sphere is 1.027 in. and the outside radius of the inner sphere is 1.000 in. Determine the capacitance of the empty cell not including the gold foil guard electrode.

Solution:

Figure 2-12(b) shows an elemental section of radius x and thickness dx within the space between the spherical plates of the cell. Let q = charge uniformly distributed on the inner spherical surface. Then the electric flux density in the elemental shell is where 4πx2(1/2 + 1/2 cos 30°) is the area of the elemental shell. The electric field intensity in the elemental shell with air as a dielectric is and the voltage between the electrodes (spherical surfaces) of the cell is The capacitance according to Eq. 2-25 is found to be and