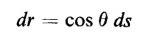| Capacitors, Magnetic Circuits, and Transformers is a free introductory textbook on the physics of capacitors, coils, and transformers. See the editorial for more information.... |

|

Home  Capacitance and Related Effects Capacitance and Related Effects  Voltage and Potential Voltage and Potential |
|||||||||||||||||||||||||||






|
|||||||||||||||||||||||||||
Voltage and Potential
When the test charge qt is moved in a direction toward the source charge, it is moved against the Coulomb force of repulsion and, energy is put into the system. On the other hand, if the test charge is moved in a direction
away from the source charge, the system gives up energy and the energy input to the system is negative. Hence, in moving the test charge qt through a differential distance ds the differential energy input to the system is expressed by
where θ is the angle between the direction of the force and the direction of the differential distance ds as shown in Fig. 2-4. The energy input to the system when the test charge is carried from a point P1 at a distance r1 from the source charge to a point P2 at a distance r2 from the source charge along any path whatsoever, as for example that illustrated in Fig. 2-5, is expressed by
From Fig, 2-4 it is evident that the scalar product ir
Hence
Equation 2-9 divided by qt yields
Equation 2-10 expresses the voltage between the points P1 and P2, the point P2 being at a potential higher than that of P1. The voltage V21 is positive.
If the point P1 in Fig. 2-5 were removed to an infinite distance then the voltage between the point P2 and point P1 would be expressed by
However, from Eq. 2-9 it is evident that the energy required to move the test charge from an infinite distance
because r1 approaches infinity. The energy associated with the test charge at an infinite distance is zero. Hence, if Eq. 2-12 is divided by qt, Eq. 2-11 results. Equation 2-11 expresses the potential of the point P2. Similarly the potential of point P1 is expressed by
If Eq. 2-13 is subtracted from Eq. 2-11 the result is the difference of potential between point P2 and point P1 and Eq. 2-10 is obtained. From this it follows that
Thus the voltage between the points P1 and P2 is simply the difference of electrical potential, the point P2 being at a higher potential than P1 This means also that the voltage V21 is positive. Similarly the potential difference obtained by subtracting Eq. 2-11 from Eq. 2-13 results in
and V12 is negative. It is evident from Eq. 2-8 that the work done in carrying a test charge from one point to another in an electric field is independent of the path along which the charge is carried. By the same token if the test charge is carried from the second point back to the first along any path whatsoever, the same amount of energy is given up. Hence
This can also be expressed as a line integral as follows
from which
Equation 2-17 states that the summation of the electric field intensity around a closed path in an electrostatic field is zero.
|
|||||||||||||||||||||||||||
Home  Capacitance and Related Effects Capacitance and Related Effects  Voltage and Potential Voltage and Potential |
|||||||||||||||||||||||||||
Last Update: 2011-01-09



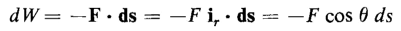

 ds is the projection of the differential distance vector ds upon r and is dr because in Eq. 2-7
ds is the projection of the differential distance vector ds upon r and is dr because in Eq. 2-7