| VIAS Encyclopedia provides a collection of tables and definitions commonly needed in science and engineering. |

|

Home  Mathematics Mathematics  Numbers Numbers  Prime Number Prime Number |
|||






|
|||
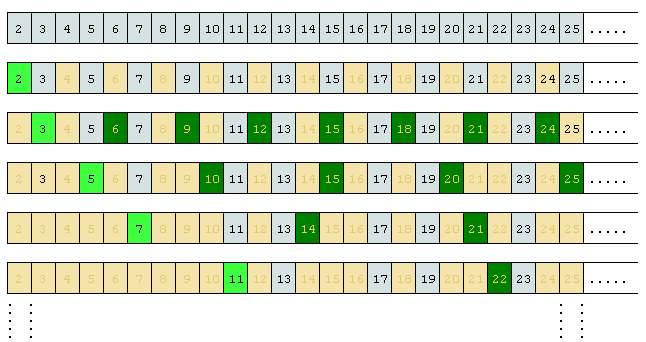
Prime NumberA prime number ("prime" for short) is a positive integer q greater than 1 which has no positive integer divisors other than 1 and q. Positive integers other than 1 which are not prime are called composite numbers. Following is a list of all prime numbers between 1 and 1000:
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997 There are many algorithms to find a prime number. One of the most widely known is the Sieve of Erastothenes. This algorithm is suitable to find the list of all primes up to a certain number p:
Please note that one can speed up the search for large prime numbers by using a list pre-computed list of all primes up to a certain bound (e.g. all primes up to 1000). Then, before testing n for primality with an elaborate method, one first checks whether n is divisible by any prime of the precomputed list.
|
|||
Home  Mathematics Mathematics  Numbers Numbers  Prime Number Prime Number |
|||
Last Update: 2004-11-27