Eigenvectors and Eigenvalues
Advanced Discussion

for its eigenvectors e and eigenvalues λ, we have to rearrange this equation (I is the identity matrix):

Note that from the last equation we cannot conclude that any of the product terms are zero. However, if we look at the determinants of this equation,

we see that a non-trivial solution is that  |A - λI|  and/or  |e|  have to be zero. So our initial condition, Ae =λe, is met when the equations above are fulfilled. The case that  |e| = 0 is the less interesting one, since this is only true if the vector e equals the zero vector o. So, for further considerations one has to look at  |A -λI| = 0. In fact, this equation is so important that it has been given a special name:
 
 

Characteristic Determinant Characteristic Function

For a given matrix A,  |A -λI| denotes its characteristic determinant in the unknown λ. The polynomial function χ(t) := |A - λI| is called the characteristic function of A. This implies that the determinant is expanded.

Example: Characteristic Determinant

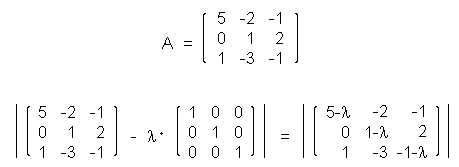
Finally, eigenvectors and eigenvalues are defined as a solution of the characteristic function:
 
 

Eigenvalue, Eigenvector

For a given matrix A and its characteristic function χ(t) = |A -λI|, the roots of the characteristic equation χ(t) = 0 are called eigenvalues (or characteristical roots) λ1, λ2, ..., λk. They meet the criterion Ae = λjej for all j in [1, k] for certain vectors ej. Those vectors ej, each of them corresponding with an eigenvalue λj, are called eigenvectors (or characteristic vectors).