VIAS Encyclopedia provides a collection of tables and definitions commonly needed in science and engineering.

Home Mathematics Matrix Algebra Matrix Determinants - Calculation of Order 2 and 3
See also: Matrix Determinant 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter

Matrix Determinants
Calculation of Order 2 and 3

The general approach how to calculate a matrix determinant is hard, requiring the calculation of many similar steps. Thus it is not recommended to calculate a determinant of matrices with an order higher than 3 without the help of a computer. For matrices of order 2 and 3 there are special rules which make it comparatively easy to determine the determinant:

Determinant of matrices of order 2

Let

[ a11
a21		 a12
a22		 ]

be an arbitrary matrix of order 2. Then its determinant is calculated as the product of the principal diagonal minus the product of the other diagonal, formally a11a22 - a12a21.

Determinant of matrices of order 3 (Sarrus' Rule)

Let

[ a11
a21
a31		 a12
a22
a32		 a13
a23
a33		 ]

be an arbitrary matrix of order 3. Then its determinant is calculated as the sum of the product of all "extended" falling (including the principal) diagonals minus the sum of the product of all "extended" rising diagonals, formally (a11a22a33 + a21a32a13 + a31a12a23) - (a31a22a13 + a21a12a33 + a11a32a23). This rule is easier to understand when we color the relevant diagonals:


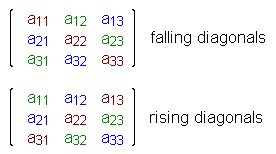
Example: determinant of a matrix of order 3

Let

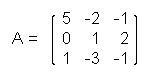
Then

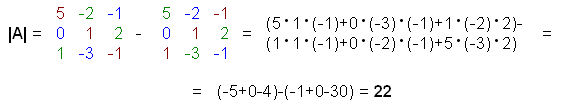
Please note that the rectangular, colored schemes do not denote actual matrices, but are only included to emphasize the rule of Sarrus.

This text is part of "Teach/Me Data Analysis" and has been included by permission of the author.

Home Mathematics Matrix Algebra Matrix Determinants - Calculation of Order 2 and 3

Last Update: 2005-01-18