Matrix Algebra
Fundamentals
The following are a few basic definitions concerning matrices.
Definition.
A matrix is a rectangularly
shaped array with m rows and n columns of m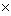 n
mathematical objects of a given basic set. The order of a matrix
is m n
mathematical objects of a given basic set. The order of a matrix
is m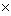 n
("m by n"). Each column and each row of a matrix defines a vector. A column
vector is nothing other than an m n
("m by n"). Each column and each row of a matrix defines a vector. A column
vector is nothing other than an m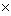 1
matrix, and a row vector is a 1 1
matrix, and a row vector is a 1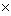 n
matrix. n
matrix.

Matrices are denoted by bold uppercase letters, e.g. A.
Matrix elements are denoted by lowercase letters subscripted by two indices,
i.e. am,n. Sometimes the comma between the indices is omitted.
The sequence of the indices is not arbitrary; the first index always denotes
the row, the second index the column. If m=n, the matrix is called a square
matrix of order n. If a matrix is square, the diagonal containing elements
of equal indices (a11, a22, ..., ann)
is called the principal diagonal of this matrix. The trace
of a matrix is the sum of all elements of the principal diagonal.
This text is part of "Teach/Me Data Analysis" and has been included by permission of the author.
|


 Mathematics
Mathematics  Matrix Algebra
Matrix Algebra  Fundamentals
Fundamentals





 Mathematics
Mathematics  Matrix Algebra
Matrix Algebra  Fundamentals
Fundamentals

 1
matrix, and a row vector is a 1
1
matrix, and a row vector is a 1