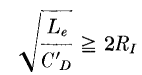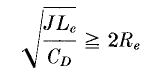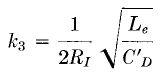False Echoes after Main Pulse

Trailing-edge oscillations are of two general types: (1) a long-term or low-frequency oscillation (see Fig. 254) dependent on capacitance C_D and pulse transformer open-circuit inductance L_e, and (2) a superposed high-frequency oscillation dependent on capacitance C_D and L'_N (= PFN inductance L_N plus pulse transformer leakage inductance L_s). If these oscillations exceed zero in the positive or main pulse direction, false "echoes" of two kinds may occur: close echoes, adjacent to the main pulse, and distant echoes which appear later at a comparatively longer time interval. Either of these cause the magnetron to give a false indication. The distant echo corresponds to oscillation (1), and the close echo superposed on this long-term backswing to oscillation (2). These are represented in Fig. 254 as oscillations f₃ and f₂, respectively. With proper attention to the circuit constants, it is possible to eliminate both types of echoes.

Fig. 254. Oscillations on pulse backswing.

The low-frequency backswing oscillation or axis is affected by C_N only while it is still in the circuit. When thyratron conduction ceases (soon after the trailing edge becomes negative) C_N is cut out of the circuit. Once this happens, the presence or absence of distant echoes is determined only by C_D in combination with L_e and R_e. Moreover, if C_N >> C_D, close echoes are also determined by C_D and L'_N, regardless of whether or not the thyratron is conducting during the close-echo interval.

Both low- and high-frequency oscillation amplitudes depend on the amount of resistance in the circuit. At instant t₁ this resistance is R_M, the magnetron resistance E/i₂ (Fig. 243), in comparison with which the transformer core-loss equivalent resistance R_e is negligibly high. After the magnetron ceases conducting, only R_e remains. During the trailing-edge interval, circuit resistance varies from R_M to R_e. Resistances R_M and R_e may be replaced by their geometric mean R₁ during the trailing-edge interval and the part of the backswing immediately following. This applies to both low- and high-frequency backswing oscillations during the interval t₂-t₁ (Fig. 254). The low-frequency or long-term axis of backswing may then be found from values of parameter k₃ determined by L_e, C_D, and R_r, as indicated in Fig. 235. If the oscillations are damped out, the impedance ratio still determines wave shape. This ratio is designated k₁, k₂, k₃, or k₄, depending on the portion of the pulse as indicated in Fig. 254.

If PFN produces an essentially square wave, front-edge wave shape at the magnetron is determined by impedance ratio

It may be shown⁽¹⁾ that if k₁ = 0.5 the magnetron voltage and current rise without oscillations to final value at t_r = 1.6 √(L_sCd). This k₁ has little influence on the trailing edge because L_s is usually small compared to L_e.

Oscillations occurring close to the trailing edge of the pulse are of frequency f₂ (determined by L'_NC'_D, where C'_D = C_DC_N/(C_D + C_N), L'_N is the sum of the transformer leakage and PFN inductance), and of amplitude determined by

This amplitude is superposed on the backswing as an axis, which, if oscillatory, has frequency f₃ determined by L_eC'_D. Since one purpose of good pulser design is the elimination of false echoes, the backswing axis considered here is always non-oscillatory. Assuming the thyratron is non-conducting for most of the backswing interval, the condition for non-oscillatory backswing is

for the close part of the backswing and

for the distant part

where L_e is the OCL at time t₁ and J is the ratio of low-frequency core permeability to pulse permeability. If

and

then

because generally

So, if the pulser is designed to prevent distant echoes, k₄ ≥ 1 and k₃ is several times the value of k₄. Time intervals influenced by these impedance ratios are illustrated in Fig. 254. In general, for a good pulse, the close part of the backswing axis follows a non-oscillatory pattern of relatively high-impedance ratio, such as those shown on Fig. 235 for k₃ > 1.

The general effect of pulse transformer magnetizing current is to depress the backswing axis. Magnetizing current does not affect the criterion for absence of false echoes k₄ > 1; hence a high ratio J is helpful in eliminating close echoes. The ratio A of magnetizing current to load current is much less for the close echo than for the distant echo because R₁ is less than R_e. Close echo Δ is approximated by

[142]

To prevent close echo, the first positive peak of oscillation should be no greater than the negative backswing axis voltage at instant t₂. Backswing axis voltage may be equated to the amplitude of the first positive oscillation peak at time t₂ in Fig. 254. This equation leads to a transcendental relation between k₂, k₃, and Δ, which is plotted in Fig. 255.⁽²⁾

Fig. 255. Borderline of close false echoes.

It will be noted that all values of k₂ in Fig. 255 are less than unity. Hence, under the conditions here assumed, there is always a certain amount of high-frequency oscillation superposed on the back-swing axis. But, if k₂ is greater than the value given by Fig. 255, there is no false close echo. Because of the approximation represented by equivalent resistance R_I, to prevent false echoes it is best if k₂ exceeds the curve value substantially. For convenience, the various impedance ratios are tabulated in Table XVII.

Table XVII. Pulser Impedance Ratios

(1)	See Pulse Generators, by Glasoe and Lebacqz, M.I.T. Radiation Laboratory Series, Vol. 5, McGraw-Hill Book Co., New York, 1948, p. 567.
(2)	This equation is developed in the author's "False Echoes in Line-Type Radar Pulsers," Proc. I.R.E., 42, 1288 (August, 1954).