Graphical Performance of Simple Magnetic Amplifiers

Since with a given core and supply frequency there corresponds a definite voltage for every flux density, and since for a given number of turns the ampere-turns per inch are proportional to current, the curves of Fig. 207 may be replotted in terms of voltage and current. We may then plot load lines on these curves in a manner similar to those in electronic amplifiers, so that the operation, efficiency, control power, etc., may all be determined from a study of these load lines.

Equation 58 indicates that the a-c voltage in a vacuum-tube circuit is divided between the load and the tube. If a resistive load is used, a straight line can be drawn on the characteristics of a vacuum tube which will form the locus of plate current and plate voltage for any given load and supply voltage. This line is called the load line, and by use of it the gain and power output of the amplifier can be determined.

A similar method can be used with magnetic amplifiers. If a linear reactor were connected in series with the load, the voltage across the load and the voltage across the reactor would add at right angles. With rectangular loop core materials, currents are not reactive in the linear sense, so that the actual load line is neither a straight line nor an ellipse. For practical calculations the straight line is used, and the results obtained are correct within small percentages if the reactor voltage and current are measured on an average-reading voltmeter and ammeter.

Fig. 208. Generalized magnetic amplifier characteristics and load line.

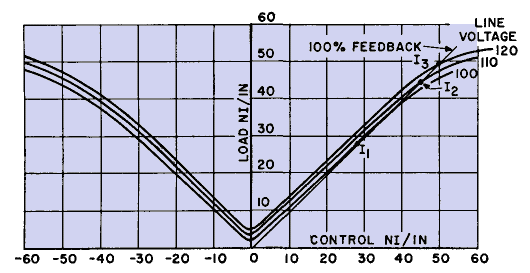
Figure 208 shows similar information to Fig. 207, except that it is for a given core. The scale of abscissas is ampere-turns, and the scale of ordinates is volts per turn. These characteristics can be used for any amplifier which uses the same cores and the same supply voltage and frequency as the amplifier on which the measurements

were made to obtain these characteristics. These characteristics can be derived for a given core from the parameters of a-c flux density, a-c magnetizing force, and d-c magnetizing force as shown to the right and top of Fig. 208. These curves then give a set of characteristics for a given core rather than for a given core material. Some error is involved if these curves are used with a different supply frequency from the one used in making the original curves. Over a narrow range of frequency the curves of Fig. 208 using the scale at the top and to the right can be used to determine the operation of a magnetic amplifier for different loads. The curves of Fig. 207 may be used for magnetic amplifier calculations in this manner. For convenience of calculation, it is usually preferable to make a set of characteristic curves for several core sizes and for each supply frequency.

An example will show how these curves can be used in the design of magnetic amplifiers. Assume that it is necessary to design an amplifier with 30 watts output using cores with E/N and NI of Fig. 208. The supply voltage is 100 volts, the load is 200 ohms, and 0.01 amp is available for use in the control winding. The characteristics show the E/N can be varied from about 1.4 to 0.2 and still stay on the linear part of the characteristic curves. The power output is equal to ΔE · ΔI which is also equal to Δ (E/N) · ΔNI, where E is the alternating voltage across the reactors, I is the alternating current through the reactors, and N is the number of turns in the load windings of the reactor. ΔNI needed for 30 watts = 30/(1.4 - 0.2) = 25 ampere-turns. Load impedance is ΔE/ΔI. A load line on Fig. 208 is (ΔE/N_L) /ΔNI = (ΔE/ΔI) (1/N_L²), where N_L = turns in load winding. For 200 ohms, the load line passes through the points E/N_L = 1.4, NI_ac = 2.5, and through E/N_L = 0.2, NI_ac = 27.5. When this line is extended to the ordinate it intersects at 1.54. This is the point of zero alternating current or of infinite reactor inductance. At this point the total supply voltage would be across the reactor. Since the supply voltage is 100 volts, 100/N = 1.54 and N_L = 65 turns. By interpolation of the d-c NI curves, we see that, for E/N = 0.2 and NI_ac = 27.5, 25 ampere-turns are necessary in the control winding. The turns in the control windings are N_cI_C/I_C = 25/0.01 = 2,500 turns. Here I_c is the current in the control winding, and N_c are the turns in the control winding. Control winding resistance is determined by the wire size. For the purpose of this example, assume that the resistance of the control winding is 500 ohms. Then the power in the control winding is 500 · I_c² = 0.05 watt. Power gain of the amplifier is power out/ power in = 30/0.05 = 600. The impedance of either the input circuit or output circuit can be changed by changing the number of turns in the respective windings. Either impedance varies with the square of the number of turns used in the winding. For example, the load line which was used for 200 ohms in the preceding example could be used for 800 ohms. The load winding would then have √(800/200) · 65 = 130 turns, and the supply voltage would be 200 volts instead of 100 for E/N = 1.54 at zero current.

Power output is proportional to the area of the rectangle of which the load line forms a diagonal. More power output can be obtained by using a load line with less slope, but gain may increase or decrease, depending upon the winding resistances and core material. In the preceding example, the load windings were assumed to be in series with the load, as in Fig. 203. This is the connection commonly used when the source is a 60-cycle a-c line. With a high impedance source, it is preferable to connect the load windings in shunt with the load. Then the ordinates of Figs. 207 and 208 correspond to load voltage at all times.

If we choose three line voltages corresponding to flux densities within the linear portions of Fig. 207, and plot the d-c control versus a-c load ampere-turns per inch, the curves of Fig. 209 result. If, instead of NI/in., average load current is plotted, Fig. 209 gives the transfer curves for a simple magnetic amplifier. The curves are symmetrical about zero ampere-turns. The difference between the transfer curve and a straight line indicates the degree of non-linearity in the amplifier for any load current. With grain-oriented core material the a-c load current is nearly independent of supply voltage for a-c inductions less than saturation. Provided that appropriate changes in scale are made, transfer curves may be plotted between load voltage and control current, or between load ampere-turns and control ampere-turns, or between combinations of these.

Load current is the result of flux excursions beyond the knee of the normal magnetization curve. In Fig. 207 the curve for zero control NI/in. is normal magnetization for the material. When direct current flows in the control windings, it sets up a constant magnetizing force in the core. Then superposed a-c magnetizing force readily causes a flux excursion beyond the knee of the curve, permeability suddenly drops, and a large current flows through the load winding. The point in the voltage cycle at which this sudden increase in current occurs depends upon the amount of direct current in the control winding. Magnetic amplifiers with steep current curves like those of Fig. 207 can be used as control relays.

Load current is usually measured with an average-reading ammeter, such as a rectifier-type instrument. This kind of ammeter is generally marked to read the rms value of sinusoidal current but actually measures the average value. Thus the ammeter reading is 0.707/0.636 = 1.11 times the average current over a half-cycle. When the meter is used to measure non-sinusoidal current, it still reads 1.11 times the average.

Fig. 209. Simple magnetic amplifier transfer curves with line-voltage variations.

Except for the slight amount of non-linearity noted in Fig. 209, the average value of ampere-turns in the load winding of each reactor equals the d-c ampere-turns in the control winding. But since the a-c ammeter reads 1.11 times this value, the load a-c NI/in. are 1.11 times the control d-c NI/in., plus the differential due to core magnetizing current. Thus, if a core had infinite permeability up to the knee of the magnetization curve and zero permeability beyond the knee, the transfer curve would be exactly linear. Oriented nickel-iron alloy cores approach this ideal and therefore are more nearly linear than other materials.