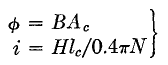Magnetizing Current

In addition to the current entering the primary because of the secondary load, there is the core exciting current I_N which flows in the primary whether the secondary load is connected or not. This current is drawn by the primary core reactance X_N and equivalent core-loss resistance R_E and is multiplied by N₂/N₁ when it is referred to the secondary side. It has two components: I_M, the magnetizing component which flows 90° lagging behind induced voltage E_s; and I_e, the core-loss current which is in phase with E_s. Ordinarily this current is small and produces negligible voltage drop in the winding.

Core-loss current is often divided into two components: eddy current and hysteresis. Eddy-current loss is caused by current circulating in the core laminations. Hysteresis loss is the power required to magnetize the core first in one direction and then in the other on alternating half-cycles. Hysteresis loss and magnetization are intimately connected, as can be seen from Fig. 5.

Fig. 5. Transformer voltage, flux, and exciting current.

Here induced voltage e is plotted against time, and core flux Φ lags e by 90°, in accordance with equation 3. This flux is also plotted against magnetizing current in the loop at the right. This loop has the same shape as the B-H loop for the grade of iron used in the core, but the scales are changed so that

[8]

where

B = core flux density in gauss
A_c = core cross-sectional area in cm²
H = core magnetizing force in oersteds
l_c = core flux path length in cm.

Current is projected from the Φ-i loop to obtain the alternating current i at the bottom of Fig. 5. This current contains both the magnetizing and the hysteresis loss components of current. In core-material research it is important to separate these components, for it is mainly through reduction of the B-H loop area (and hence hysteresis loss) that core materials have been improved. Techniques have been developed to separate the exciting current components, but it is evident that these components cannot be separated by current measurement only. It is nevertheless convenient for analysis of measurements to add the loss components and call their sum I_E, and to regard the magnetizing component I_M as a separate lagging current, as in Fig. 3. As long as the core reactance is large, the vector sum I_N of I_M and I_E is small, and the non-sinusoidal shape of I_N does not seriously affect the accuracy of Fig. 3.

Core flux reactance may be found by measuring the magnetizing current, i.e., the current component which lags the applied voltage 90° with the secondary circuit open. Because of the method of measurement, this is often called the open-circuit reactance, and this reactance divided by the angular frequency is called the open-circuit inductance. The secondary and primary winding leakage reactances are found by short-circuiting the secondary winding and measuring the primary voltage with rated current flowing. The component of primary voltage which leads the current by 90° is divided by the current; this is the sum of the leakage reactances, the secondary reactance being multiplied by the (turns ratio)², and is called the short-circuit reactance.

Practical cases sometimes arise where the magnetizing component becomes of the same order of magnitude as I_L. Because current I_M flows only in the primary, a different equivalent circuit and vector diagram are necessary, as shown in Fig. 6.

Fig. 6. (a) Equivalent circuit and (b) vector diagram for transformer with high magnetizing current.

Note that the leakage reactance voltage drop has a marked effect upon the load voltage, and this effect is larger as I_m increases relative to I_L. Therefore, the statement that IX voltage drop causes negligible difference between secondary induced and terminal voltages in transformers with resistive loads is true only for small values of exciting current. Moreover, the total primary current I₁ has a largely distorted shape, so that treating the IR and IX voltage drops as vectors is a rough approximation. For accurate calculation of load voltage with large core exciting current, a point-by-point analysis would be necessary.