| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Vector Calculus Vector Calculus  Surface Area and Surface Integrals Surface Area and Surface Integrals  Surface Integral Surface Integral |
|






|
|
Surface Integral
DEFINITION Let S be an oriented surface z = g(x, y) over D and let F(x, y, z) = Pi + Qj + Rk be a vector field defined on S. The surface integral of F over S is defined by
+ if the top side of S is positive, - if the top side of S is negative. Thus a change in orientation of S changes the sign of the surface integral. JUSTIFICATION We show that this definition corresponds to the intuitive concept of flux, or net rate of fluid flow, across a surface. Suppose S is oriented so that the top surface of S is positive. Let B(D) be the flux across the part of S over a region D. Consider an element of area ΔD and let ΔS be the area of S over ΔD. Then ΔS is almost a piece of the tangent plane. The component of fluid flow perpendicular to ΔS is given by the scalar product F · N where N is the unit normal vector on the top side of ΔS (Figure 13.5.7). Thus the flux across ΔS is ΔB ≈ F · N ΔS (compared to ΔA).
Figure 13.5.7 This suggests the surface integral notation
Let us find F, N, and ΔS. The vector F at (x, y, z) is (1) F(x,y,z) = Pi + Qj + Rk. From Section 13.1, one normal vector at (x, y, z) is
The unit normal vector N on the top side of ΔS has positive k component and length one, so (2)
From our study of surface areas, (3)
When we substitute Equations 1-3 into F · N ΔS, the radicals cancel out and we have
Using the Infinite Sum Theorem we get the surface integral formula
|
|
Home  Vector Calculus Vector Calculus  Surface Area and Surface Integrals Surface Area and Surface Integrals  Surface Integral Surface Integral |
|
Last Update: 2010-11-25


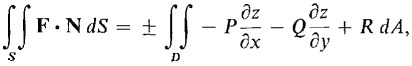




 (compared to ΔA).
(compared to ΔA). (compared to ΔA).
(compared to ΔA).