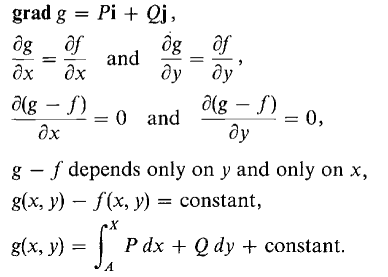| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Vector Calculus Vector Calculus  Independence of Path Independence of Path  Proof Of Theorem 1 Proof Of Theorem 1 |
|






|
|
Proof of Theorem 1
Figure 13.3. PROOF OF THEOREM 1 We must find a potential function for Pi + Qj. Assume ∂P/∂y = ∂Q/∂x. Pick a point (a, b) in D, and let f(x0, y0) be the line integral of Pi + Qj on the rectangular curve C from (a, b) to (a, y0) to (x0, y0) (Figure 13.3.7). Thus
By the Lemma,
Thus
(i) Let C have the parametric equations x = g(t) y = h(t), c1 ≤ t ≤ c2. Then A = (g(cl), h(c1)) and B = (g(c2), h(c2)). By the Chain Rule,
Then
A similar computation works for piecewise smooth curves. This proves (i). (ii) Define f(x, y) by
where A = (a, b), X = (x, y). Let C be the rectangular curve from (a, b) to (a, y) to (x, y). Then
We already showed in the proof of Theorem 1 that this function f(x, y) is a potential function for Pi + Qj. To complete the proof we note that the following are equivalent.
|
|
Home  Vector Calculus Vector Calculus  Independence of Path Independence of Path  Proof Of Theorem 1 Proof Of Theorem 1 |
|
Last Update: 2006-11-25





 and
and