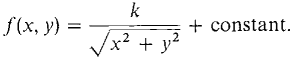Example 4

EXAMPLE 4

An object at the origin (0, 0) has a gravity force field with magnitude proportional to l/(x² + y²) and the direction of -xi -yj Show that this force field is conservative and find a potential function.

The force vector is

for some constant k. F(x, y) is undefined at (0,0) but is a vector field on the open rectangle 0 < x.

Therefore F is conservative.

Any choice of the constant will give a potential function. The same method works on the open rectangle x < 0.

An exact differential equation is an equation of the form

P(x,y)dx + Q(x,y)dy = 0, where ∂P/∂y - ∂Q/∂x. Exact differential equations can be solved using Theorem 2.