| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Vector Calculus Vector Calculus  Line Integrals Line Integrals  Examples Examples  Example 2: Work Done by a Force Vector Along a Curve Example 2: Work Done by a Force Vector Along a Curve |
|






|
|
Example 2: Work Done by a Force Vector Along a Curve
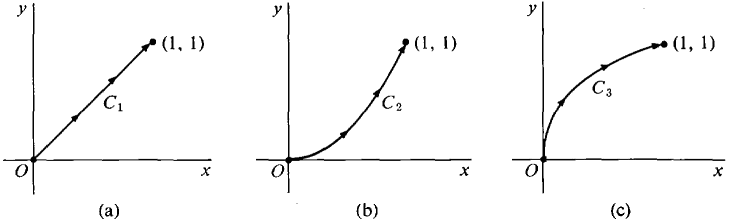
EXAMPLE 2 Let the force vector F be F = -yi + xj. F is perpendicular to the position vector xi + yj but has the same length as xi + yj. Find the work done by F along the following curves, shown in Figure 13.2.8, from (0, 0) to (1, 1): (a) C1: The line y = x, 0 ≤ x ≤ 1. (b) C2: The parabola y = x2,0 ≤ x ≤ 1. (c) C3: The curve
Figure 13.2.8 (a) Put x = t, y = t.
The work is zero because the force F is perpendicular to dS along C1. (b) Put x = t,y = t2.
(c) Put x = t3, y = t.
|
|
Home  Vector Calculus Vector Calculus  Line Integrals Line Integrals  Examples Examples  Example 2: Work Done by a Force Vector Along a Curve Example 2: Work Done by a Force Vector Along a Curve |
|
Last Update: 2006-11-20


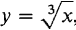 , 0 ≤ x ≤ 1.
, 0 ≤ x ≤ 1.