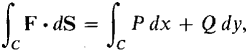| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Vector Calculus Line Integrals Definitions |
|
 Search the VIAS Library | Index
|
  |
Definitions
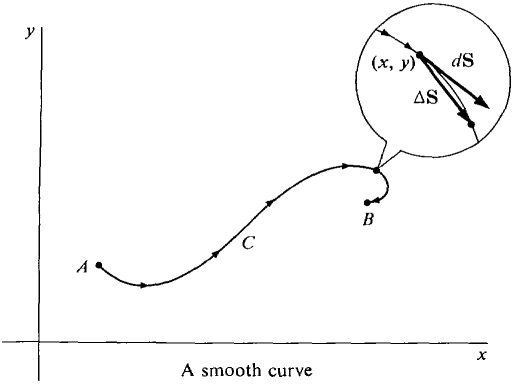
DEFINITION A smooth curve from A to B is a curve C given by parametric equations x = g(s), y = h(s) 0 ≤ s ≤ L, where:
We call A the initial point and B the terminal point of C. A smooth curve from A to B is also called a directed curve, and is drawn with arrows. Given s and an infinitesimal change Δs = ds, we let, Δx = g(s + Δs) - g(s), dx = g'(s) ds, Δy = h(s + Δs) - h(s), dy = h'(s) ds, ΔS = Δxi + Δyj, dS = dxi + dyj. Thus ΔS is the vector from the point (x, y) to (x + Δx, y + Δy) on C, and dS is an infinitesimal vector tangent to C at (x, y) (Figure 13.2.4).
Figure 13.2.4 DEFINITION Let F(x, y) = P(x, y)i + Q(x, y)j be a continuous vector valued function on an open rectangle D and let C be a smooth curve in D. The line integral of F along C,
is defined as the definite integral
Notice that the inner product of F and dS is F · dS = (Pi + Qj) · (dxi + dyj) = P dx + Q dy. This is why we use both notations ∫C F · dS and ∫C P dx + Q dy for the line integral. DEFINITION The work done by a continuous force vector F(x, y) along a smooth curve C is given by the line integral
JUSTIFICATION We can justify this definition by using the Infinite Sum Theorem from Chapter 6. Let W(u, v) be the work done along C from s = u to s = v (Figure 13.2.5). Then W(u, v) has the Addition Property, because the work done from u to v plus the work done from v to w is the work done from u to w. On an infinitesimal piece of C from s to s + Δs, the work done is A W ≈ F(x, y) · ΔS ≈ F(x, y) · dS (compared to Δs). But
Figure 13.2.5 By the Infinite Sum Theorem,
|
|
| Home Vector Calculus Line Integrals Definitions |
|
Last Update: 2010-11-25