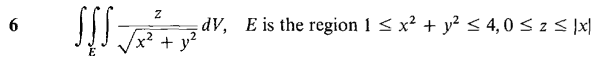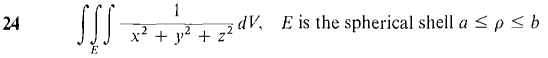Problems

In Problems 1- 6, evaluate the integral using cylindrical coordinates.

7            Find the mass of an object in the shape of a cylinder of radius b and height h whose density is equal to the distance from the axis.

8            Find the mass of an object in the shape of a cylinder of radius b and height h whose density is equal to the distance from the base.

9            Find the mass of an object in the shape of a cone of radius b and height h whose density is equal to the square of the distance from the axis.

10            Find the mass of an object in the shape of a cone of radius b and height h whose density is equal to the sum of the distance from the base and the distance from the axis.

11             Find the center of mass of an object of constant density filling the region above the paraboloid z = x² + y² and below the plane z = 1.

12            Find the center of mass of an object of constant density filling the region

13            Find the moment of inertia of an object of constant density k in the cylinder 0 ≤ r ≤ b, - c ≤ z ≤ c, about the x-axis.

14            Find the moment of inertia of an object of constant density k in the cylindrical shell a ≤ r ≤ b, -c≤z≤c, about the z-axis.

15            Find the moment of inertia of an object of constant density k in a cone of radius b and height h about its axis.

16            Find the moment of inertia of an object of constant density k in a cone of radius b and height h about a line through its apex and perpendicular to its axis.

In Problems 17-24, evaluate the integral using spherical coordinates.

25            Find the volume of the spherical shell a ≤ ρ ≤ b.

26             Find the volume of the spherical box α₁ ≤ θ ≤ α₂, β₁ ≤ φ ≤ β₂, c₁ ≤ ρ ≤ c₂-

27            Find the volume of the region above the cone φ = β and inside the sphere ρ = b cos φ.

28            Find the volume of the spherical region 0 ≤ θ ≤ 2π, 0 ≤ φ ≤ π, 0 ≤ ρ ≤ sin φ.

29            Find the mass of an object in the shape of a sphere of radius c whose density is equal to the distance from the center.

30            Find the mass of a spherical shell a ≤ ρ ≤ b whose density is equal to the reciprocal of the distance from the center.

31             Find the moment of inertia of a spherical object of radius b and constant density k about a diameter of the sphere.

32            Find the moment of inertia of a spherical shell a ≤ ρ ≤ b of constant density k about any diameter.

33            A hole of radius a is bored through a sphere of radius b, and the surface of the hole passes through the center of the sphere, a = ½b. Find the volume removed.

34            A hole of radius a is bored through a cone of height h and base of radius b, and the axis of the cone is on the surface of the hole (a ≤ ½b). Find the volume removed.

35            Find the center of mass of a hemisphere of constant density and radius b.

36            Find the moment of inertia of an object of constant density k in the ellipsoid

about the z-axis. Hint: Change variables x₁ = x/a, y₁ = y/b, z₁ = z/c and use spherical coordinates.