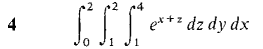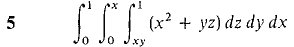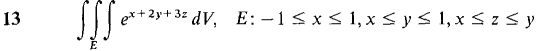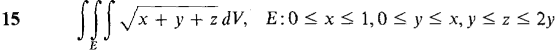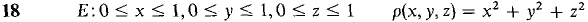Problems

In Problems 1-8, evaluate the iterated integral.

In Problems 9-16, evaluate the triple integral.

In Problems 17-26, find (a) the mass, (b) the center of mass, (c) the moments of inertia about the three coordinate axes, of an object with density ρ(x, y, z) filling the region E.

23            E is the tetrahedron with vertices at (0,0,0), (a, 0,0), (0, b, 0), (0,0, c), ρ(x, y, z) = k.

24            £ is the tetrahedron with vertices (0,0,0), (1,0,0), (1,1,0), (1,0,1), ρ(x, y, z) = x + y + z.

25            E is the rectangular box 0 ≤ x ≤ a, 0 ≤ y ≤ b, 0 ≤ z ≤ c, ρ(x, y, z) = k.

26                   E is the rectangular box - a ≤ x ≤ a, -b ≤ y ≤ b, -c ≤ z ≤ c, ρ(x, y, z) = k.