| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Multiple Integrals Multiple Integrals  Triple Integrals Triple Integrals  Examples Examples  Example 4 Example 4 |
|||||||






|
|||||||
Example 4
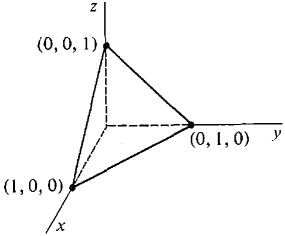
An object has constant density and the shape of a tetrahedron with vertices at the four points (0,0,0), (1,0,0), (0,1,0), (0,0,1). Find the center of mass.
|
|||||||
Home  Multiple Integrals Multiple Integrals  Triple Integrals Triple Integrals  Examples Examples  Example 4 Example 4 |
|||||||
Last Update: 2006-11-15


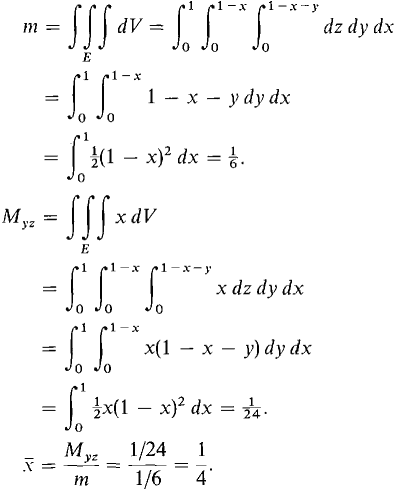
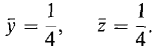 The center of mass is
The center of mass is