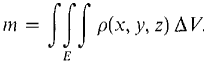| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Multiple Integrals Triple Integrals Mass of a Region |
|
 Search the VIAS Library | Index
|
  |
Mass of a Region
Here are some applications of the triple Infinite Sum Theorem. Perhaps the simplest physical interpretation of the triple integral is mass as the triple integral of density. DEFINITION The mass of an object filling a solid region E with continuous density ρ(x, y, z) is
JUSTIFICATION At every point of an element of volume ΔE the density is infinitely close to ρ(x, y. z), so the element of mass is Δm ≈ ρ(x, y, z) ΔV (compared to ΔV). (See Figure 12.6.8.) By the Infinite Sum Theorem,
Figure 12.6.8
|
|
| Home Multiple Integrals Triple Integrals Mass of a Region |
|
Last Update: 2010-11-25