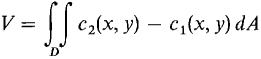The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Multiple Integrals Triple Integrals Corollary
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Corollary

COROLLARY

The volume of a region E in space is equal to the triple integral of the constant 1 over E as illustrated in Figure 12.6.6,

12_multiple_integrals-343.gif

12_multiple_integrals-344.gif

Figure 12.6.6

PROOF

E is the solid over the plane region D given by

a1 ≤ x ≤ a2, b1(x) ≤ y ≤ b2(x)

between the surfaces z = c1(x, y) and z = c2(x, y). By definition of the volume between two surfaces,

12_multiple_integrals-345.gif

Using the Iterated Integral Theorem,

12_multiple_integrals-346.gif

We now come to the Infinite Sum Theorem for triple integrals, which is, again, the key result for applications.

We shall use Δx, Δy, and Δz for positive infinitesimals. By an element of volume we mean a rectangular box ΔE with sides Δx, Δy, and Δz (Figure 12.6.7). The volume of ΔE is

ΔV = ΔxΔyΔz.

12_multiple_integrals-347.gif

Figure 12.6.7
Home Multiple Integrals Triple Integrals Corollary

Last Update: 2010-11-25