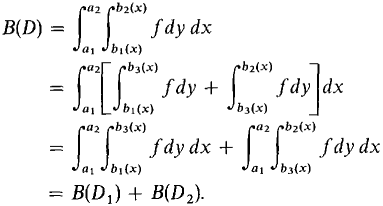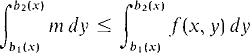The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Multiple Integrals Iterated Integrals Proof of the Iterated Integral Theorem
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Proof of the Iterated Integral Theorem

PROOF OF THE ITERATED INTEGRAL THEOREM

For any region D, let B(D) be the iterated integral over D. Our plan is to prove that B has the Addition and Cylinder Properties, so that by the Uniqueness Theorem B(D) will equal the double integral.

PROOF OF ADDITION PROPERTY

Case 1

Let D be divided into D1 and D2 as in Figure 12.2.8(a). By the Addition Property for single integrals,

12_multiple_integrals-102.gif

 12_multiple_integrals-104.gif
Case 2

Let D be divided into D1 and D2 as in Figure 12.2.8(b). Then

12_multiple_integrals-103.gif

 12_multiple_integrals-105.gif
    Figure 12.2.8(a), (b)

 

PROOF OF CYLINDER PROPERTY

Let m be the minimum value and M the maximum value of f(x, y) on D For each fixed value of x.

12_multiple_integrals-106.gif

Integrating from a1 to a2,

12_multiple_integrals-107.gif

But

12_multiple_integrals-108.gif

Therefore

mA ≤ B(D).

By a similar argument,

B(D) ≤ MA.

Since B has both the Addition and Cylinder Properties,

12_multiple_integrals-109.gif
Home Multiple Integrals Iterated Integrals Proof of the Iterated Integral Theorem

Last Update: 2006-11-05