The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Multiple Integrals Iterated Integrals Examples Example 5
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Example 5

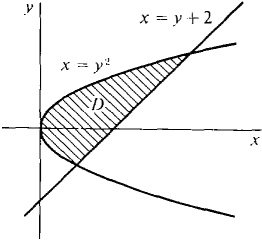
Let D be the region bounded by the curves

x = y2, x = y + 2. Evaluate the double integral ∫∫D xy dA.

Step 1

The region D is sketched in Figure 12.2.7.

12_multiple_integrals-98.gif

Figure 12.2.7

Step 2

Find inequalities for D. To do this we must find the points where the curves x = y2, x = y + 2 intersect. Solving for y and then x, we see that they intersect at (1,-1), (4,2).

We see from the figure that D is a region in either the (x, y) plane or the (y, x) plane. However, the boundary curves are simpler in the (y, x) plane. D is the region

-1 ≤ y ≤ 2, y2 ≤x≤ y + 2.

Step 3

Set up the iterated integral and evaluate.

12_multiple_integrals-99.gif

12_multiple_integrals-100.gif

12_multiple_integrals-101.gif

Home Multiple Integrals Iterated Integrals Examples Example 5

Last Update: 2006-11-15