| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Partial Differentiation Partial Differentiation  Maxima and Minima Maxima and Minima  Examples Examples  Example 6 Example 6 |
|||||||||||






|
|||||||||||
Example 6
Find the maximum and minimum, if any, of the function
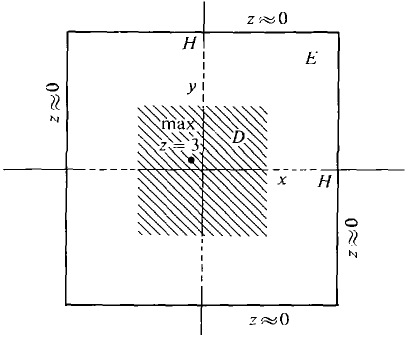
CONCLUSION z has a maximum of 3 at the critical point (-⅔, ⅓). z has no minimum. The region E is sketched in Figure 11.7.12.
Figure 11.7.12
|
|||||||||||
Home  Partial Differentiation Partial Differentiation  Maxima and Minima Maxima and Minima  Examples Examples  Example 6 Example 6 |
|||||||||||
Last Update: 2006-11-15



 = -[2(x + y) + 2(x + l)][(x + y)2 + (x + 1)2 + y2] -2,
= -[2(x + y) + 2(x + l)][(x + y)2 + (x + 1)2 + y2] -2, 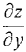 = -[2(x + y) + 2y][(x + y)2 + (x + 1)2 + y2] -2.
= -[2(x + y) + 2y][(x + y)2 + (x + 1)2 + y2] -2.