Unbounded Open Regions

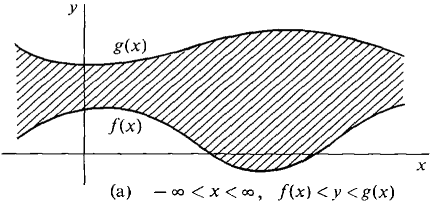
We shall now develop a method for finding maxima and minima of functions defined on open regions.

A bounded open region D is a set of points given by strict inequalities

a < x < b, f(x) < y < g(x)

where f and g are continuous and f(x) < g(x) on (a, b). A closed region with its boundary removed is a bounded open region.

We shall also consider unbounded open regions, which are given by strict inequalities where one or more of a, b, f(x), g(x) are replaced by infinity symbols. For example, the following are unbounded open regions:

(1)     -∞ < x < ∞, f(x) < y < g(x).

(2)    0 < x < ∞, 0 < y < ∞.

(3)    The whole plane -∞ < x < ∞, -∞ < y < ∞.

Unbounded open regions are pictured in Figure 11.7.8.

Figure 11.7.8 Unbounded Open Regions

A smooth function whose domain is an open region may or may not have a maximum or minimum. Many problems have at most one critical point, and we shall concentrate on that case. The method can readily be extended to the case of two or more critical points. The Critical Point Theorem holds for open regions as well as closed regions. The corollary below shows how it can be used in maximum or minimum problems.

This corollary can be used to show certain functions do not have a maximum or minimum. If we are sure a function has a maximum or minimum, the corollary can be used to find it.

Example 3: Neither Maximum Nor Minimum

Example 4: No Maximum

Example 5: Minimum Existing