| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Partial Differentiation Partial Differentiation  Total Differentials and Tangent Planes Total Differentials and Tangent Planes  Problems Problems |
|






|
|
Problems
In Problems 1-16, find the increment and total differential.
In Problems 17-22, express Δz in the form Δz = dz + ε1 Δx + ε2 Δy. In Problems 23-40 find the tangent plane at the given point.
41 Show that if z is a linear function of x and y, z = ax + by + c, then Δz = dz at every point (x, y). 42 Let f(x,y) =
43 Let f(x, y) =
44 Let f(x, y) = |xy|. Show that at (0,0),
45 Let f(x, y) = |x| + |y|. Show that at (0, 0),
|
|
Home  Partial Differentiation Partial Differentiation  Total Differentials and Tangent Planes Total Differentials and Tangent Planes  Problems Problems |
|
Last Update: 2010-11-25











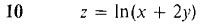

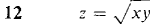



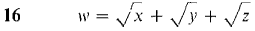
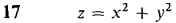

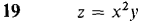
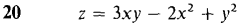








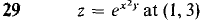

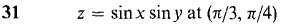




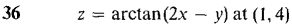



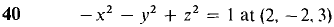

 . Prove that at the point (0,0),
. Prove that at the point (0,0),