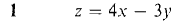Problems

In Problems 1-28, find the partial derivatives.

In Problems 29-40 find the partial derivatives at the given point.

41            A point P(x, y) at (1,2) is moving at unit speed in the x direction. Find the rate of change of the distance from P to the origin.

42            A point P(x, y) at (1, 2) is moving at unit speed in the y direction. Find the rate of change of the distance from P to the point (5, - 1).

43            A point P(x, y, z) is moving at unit speed in the x direction. Find the rate of change of the distance from P to the origin when P is at (1,2, 2).

44            A point P(x, y, z) is moving at unit speed in the z direction. Find the rate of change of the distance from P to the origin when P is at (3, √3, 2).

45            Find b and c if for all x and y,

z = x² + bxy + cy² and

46            Find b if for all x and y

z = sin x sin y + b cos x cos y and

47            It is found that the cost of producing x units of commodity one and y units of commodity two is

C(x,y)= 100 + 3x + 4y-

Find the partial marginal costs with respect to x and y, ∂C/∂x and ∂C/∂y.

48           When a certain three commodities are produced in quantities x. y, and z respectively,

it is found that they can be sold at a profit of

P(x, y, z) = 100x + 100y + yz - xy - z². Find the marginal profits with respect to x, y and z; i.e., ∂P/∂x, ∂P/∂y, and ∂P/∂z.