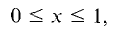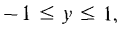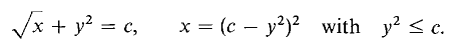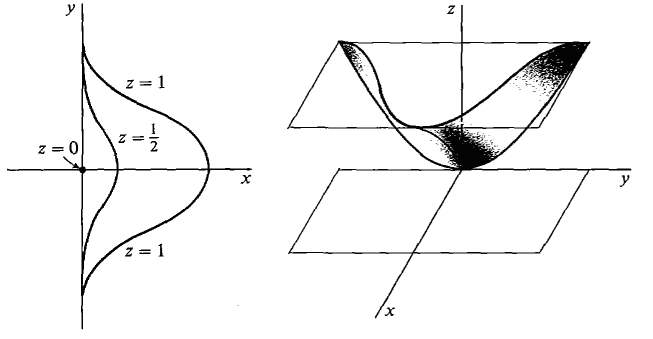| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Partial Differentiation Partial Differentiation  Surfaces Surfaces  Examples Examples  Example 8: 'Beaker Spout' Shaped Curve Example 8: 'Beaker Spout' Shaped Curve |
|||||||||






|
|||||||||
Example 8: 'Beaker Spout' Shaped Curve
Graph the function
|
|||||||||
Home  Partial Differentiation Partial Differentiation  Surfaces Surfaces  Examples Examples  Example 8: 'Beaker Spout' Shaped Curve Example 8: 'Beaker Spout' Shaped Curve |
|||||||||
Last Update: 2006-11-15


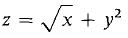 where
where