| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Vectors Vectors  Vector Derivatives Vector Derivatives  Problems Problems |
|






|
|
Problems
In Problems 1-9 find the derivative.
10 Find the line tangent to the curve X = sin2ti + cos2tj + sin t cos tk at t = π/3. 11 Find the line tangent to the curve X = ti + t2j + t3k at the point (1, 1, 1). 12 Find the line tangent to the cycloid X = (t - sin t)i + (1 - cos t)j at t = π/4. In Problems 13-25 find the velocity, speed, and acceleration.
20 A point on the rim of a wheel of radius one in the (x, y) plane which is spinning counterclockwise at one radian per second and whose center at time t is at (t, 0). (At t = 0, S = i.) 21 A bug which is crawling outward along a spoke of a wheel at one unit per second while the wheel is spinning at one radian per second. The center of the wheel is at the origin, and at t = 0, the bug is at the origin and the spoke is along the x-axis. (A spiral of Archimedes.) 22 The point at distance one from the origin in the direction of the vector
23 A car going counterclockwise around a circular track x2 + y2 = 1 with speed |2t| at time t. At t = 0 the car is at (1,0). 24 A point moving at speed one along the parabola y = x2, going from left to right. (S = 0 at t = 0.) 25 A point moving at speed y along the curve y = ex going from left to right. (S = j at t = 0.) In Problems 26-33 find the length of the given curve.
In Problems 34-37 find the position vector of a particle with the given velocity vector and initial position.
38 Find the position vector of a particle whose acceleration vector at time r is A = i + tj + etk, if at t = 0 the velocity and position vectors are both zero. 39 Find the position vector S if A = sin ti + cos tj + k, and at t = 0, V = 0 and S = 0. 40 Show that if U is the unit vector of X, then
41 Show using the Chain Rule that if X is the position vector of a curve and s is the length from 0 to t, then dX/ds is a unit vector tangent to the curve. 42 Suppose a particle moves so that its speed is constant and its distance from the origin at time t is et. Show that the angle between the position and velocity vectors is constant. 43 Prove that if F(t) is perpendicular to a constant vector C for all t, then F'(t) is also perpendicular to C. 44 Prove that if F(t) is parallel to a constant vector C for all t, then F'(t) is also parallel to C. 45 Prove the following differentiation rule for scalar multiples:
46 Prove the vector product rule
|
|
Home  Vectors Vectors  Vector Derivatives Vector Derivatives  Problems Problems |
|
Last Update: 2006-11-25



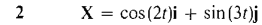


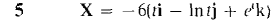




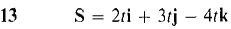




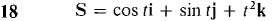

 t > 0.
t > 0.













