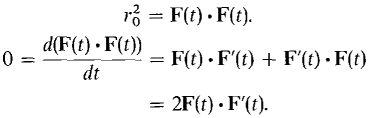| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Vectors Vector Derivatives Corollary |
|
 Search the VIAS Library | Index
|
  |
Corollary
COROLLARY Suppose X = F(t) is a curve whose distance |F(t)| from the origin is a constant r0. Then the derivative F'(t) is perpendicular to F(t) whenever F'(t) ≠ 0. PROOF We use the Inner Product Rule. For all t,
Therefore F(t) · F'(t) = 0, so F(t) ⊥ F'(t), as shown in Figure 10.7.6.
Figure 10.7.6 We see from the corollary that if a particle moves with constant speed |V| = v0, then its acceleration vector is always perpendicular to the velocity vector (Figure 10.7.7).
Figure 10.7.7 Motion with Constant Speed
|
|
| Home Vectors Vector Derivatives Corollary |
|
Last Update: 2006-11-06