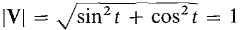| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Vectors Vectors  Vector Derivatives Vector Derivatives  Examples Examples  Example 4: Velocity, Speed, Acceleration Around the Unit Circle Example 4: Velocity, Speed, Acceleration Around the Unit Circle |
|






|
|
Example 4: Velocity, Speed, Acceleration Around the Unit Circle
Find the velocity, speed, and acceleration of a particle which moves around the unit circle with position vector S = cos ti + sin tj.
Figure 10.7.3 Velocity: V = - sin ti + cos tj. Speed:
Acceleration: A = - cos ti - sin tj. As Figure 10.7.3 shows, the velocity V is tangent to the circle and the acceleration A points to the center of the circle.
|
|
Home  Vectors Vectors  Vector Derivatives Vector Derivatives  Examples Examples  Example 4: Velocity, Speed, Acceleration Around the Unit Circle Example 4: Velocity, Speed, Acceleration Around the Unit Circle |
|
Last Update: 2006-11-15