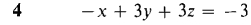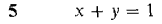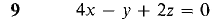Problems

In Problems 1-12 find the points, if any, where the plane meets the x, y, and z axes, and sketch the plane.

Find a scalar equation for the plane described in Problems 14-32

14            The plane with normal vector N = i + j - k and position vector P = 2i + k.

15            The plane with normal vector N = j + 2k and position vector P = i + 3j - 6k.

16            The plane through the point (1, 5, 8) with normal vector N = Si + j - k.

17            The plane through the origin with normal vector N = i + j + 2k.

18            The plane with position vector P = i - j and direction vectors C = i + j + k, D = i - j - k.

19            The plane through the point (1, 2, 3) with direction vectors C = i, D = j + k.

20            The plane through the points A(0, 4, 6), B(5, 1,-1), C(2, 6, 0).

21             The plane through the points A(5, 0, 0), B(0, 1, 0), C(0, 0, -4).

22            The plane through the points A(4, 9, -6), B(6, 6, 6), C(l, 10, 0).

23            The plane through the point A(l, 2, 4) containing the line

X = 2i + 3j + k + t(i - k).

24            The plane through the point A(0, 5, 1) containing the line

X = i + t(3i - j + k).

25            The plane through the point A(5, 0, 1) perpendicular to the line

X = i + j + k + t(2i + j + 3k).

26            The plane through the origin perpendicular to the line

X = t(5i - j + 6k).

27            The plane through the point A(A, 10, -3) parallel to the plane x + y - 2z = 1.

28            The plane through the origin parallel to the plane 4x + y + z = 6.

29            The plane containing the line X = i + j - k + t(3i + k) and perpendicular to the plane

2x - y + z = 3.

30            The plane containing the line X = 3j + t(5i + j - 6k) and perpendicular to the plane

x + y + z = 0.

31             The plane containing the line X = 3i + j + k + t(i - 6k) and parallel to the line X = i + j + f(3i + 4j + k).

32            The plane containing the x-axis and parallel to the line X = t(i + 2j - k).

In Problems 33-36, test for perpendiculars and parallels.

33            The planes x - 3y + 2z = 4, -2x + 6y - 4z = 0.

34            The planes 4x + 3y - z = 6, x + y + 7z = 4.

35            The plane -x + y - 2z = 8 and the line X = 2i + k + t(3i - j + k).

36            The plane x + y + 3z = 10 and the line X = 3j + t(i + 2j - k).

In Problems 37-42 find a vector equation for the given line.

37            The line through P(5, 3, -1), perpendicular to the plane x - y + 3z = 1.

38            The line through the origin, perpendicular to the plane x - y + z = 0.

39            The line of intersection of the planes x + y + z = 0, x - y + 2z = 1.

40            The line of intersection of the planes 2x + 3y - 4z = 1, x + z = 4.

41             The line of intersection of the planes x + y = 1, y - z = 2.

42            The line of intersection of the planes x - 2y + 3z = 0, z = -2.

In Problems 43-49, find the coordinates of the given point.

43            The point where the line X = 3i + j + k + t( -i + 3j - k) intersects the plane x + 2y - z = 4.

44            The point where the line X = i + k + t(j + k) intersects the plane x + 2y = - 3.

45            The point where the line X = t(i - 2k) intersects the plane x - 3y + 2z = 4.

46            The point P on the plane x + 3y + 6z = 6, nearest to the origin. Hint: The line from the origin to P must be perpendicular to the plane.

47            The point P on the plane x + y + z = 1, nearest to the point A(-1, 2, 3).

48            The point P on the line X = i + 2j + 3k + t(i - j + k) nearest to the origin. Hint: P must be on the plane through the origin perpendicular to the line.

49            The point P on the line X = j + t(i + 3k) nearest to the point A(1, 2, 3).

50           Prove that any three points which are not all on a line determine a plane.

51            Prove that if a line and plane are parallel and have at least one point in common then

the line is a subset of the plane.

52           Prove that if two parallel planes have at least one point in common then they are equal.

53           Let p be a plane with normal vector N. Prove that every vector D perpendicular to N is

a direction vector of p.

54           Given a plane p and a line L not perpendicular to p, prove that there is a unique plane q

which contains L and is perpendicular to p.