Example 11: Intersection Point Between a Line and a Plane

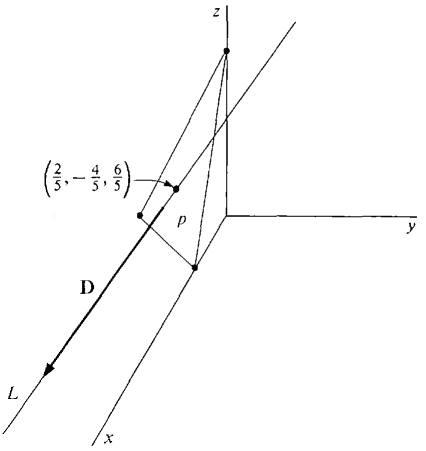
Find the point at which the line X = i - j + k + t(3i - j - k) intersects the plane 3x - 2y + z = 4.

The line has the parametric equations

x = 1 + 3t,        y = -1 -t,       z = 1 - t.

We substitute these in the equation for the plane and solve for t.

3(1 + 3t) - 2(-1 - t) + (1 - t) = 4,

6 + 10t = 4, t = -1/5

Therefore the point of intersection is given by the parametric equations for the line at t = -1/5;

x = 2/5,             y =-4/5,            z = 6/5,

(see Figure 10.5.13).

Figure 10.5.13