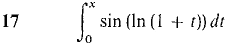Problems;

In Problems 1-8, find MacLaurin's Formula for f(x), and use it to approximate f(½) within 0.01. (If a hand calculator is available, the approximations should be found within 0.0001.)

In Problems 9-18 find the first two nonzero terms in MacLaurin's Formula and use it to approximate f(⅓).

19            Find Taylor's Formula for f(x) = e^x in powers of x - 2.

20            Find Taylor's Formula for f(x) = ln x in powers of x - 10.

21            Find Taylor's Formula for f(x) = x^p in powers of x - 1, where p is a constant real number.

22            Find Taylor's Formula for f(x) = sin x in powers of x - π.