| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Taylor's Formula Taylor's Formula  Taylor polynomials Taylor polynomials |
|||||||






|
|||||||
Taylor polynomials
9.10 TAYLOR's FORMULA If we wish to express f(x) as a power series in x - c, we need two things: (1) A sequence of polynomials which approximate f(x) near x = c, (1) a0, a0 + a1(x - c), ...,a0 + a1(x - c) + ... + an(x - c)n,.... (2) An estimate for the error En between f(x) and the nth polynomial, (2) f(x) = a0 + a1(x - c) + ... + an(x - c)n + En. In the last section the formula
was used to obtain power series approximations. A much more general formula of this type is Taylor's Formula. In Taylor's Formula the nth polynomial Pn(x) is chosen so that its value and first n derivatives agree with f(x) at x = c. The tangent line at x = c, P1(x) = f(c) + f'(c)(x - c), has the same value and first derivative as f(x) at x = c. A polynomial of degree two with the same value and first two derivatives as f(x) at c is
P1(x) and P2(x) are the first and second Taylor polynomials of f(x) (see Figure 9.10.1).
Figure 9.10.1 First and Second Taylor Polynomials To continue the procedure we need a formula for the nth derivative of a polynomial. LEMMA 1 Let P(x) be a polynomial in x - c of degree n. P(x) = a0 + a1(x - c) + a2(x - c) + ... + an(x - c)n. For each m ≤ n, the mth derivative of P(x) at x = c divided by m! is equal to the coefficient am,
PROOF Consider one term ak(x - c)k. Its mth derivative is
At x = c, the mth derivative of ak(x - c)f is: 0 if in < k, m! am if in = k, 0 if in > k. It follows that P(m)(c) = m! am. This lemma shows us how to find a polynomial P(x) whose value and first n derivatives agree with f(x) at x = c. The mth coefficient of P(x) must be DEFINITION Let f(x) have derivatives of all orders at x = c. The nth Taylor polynomial of f(x) at x = c is the polynomial
By Lemma 1, Pn(x) is the unique polynomial of degree n whose value and first n derivatives at x = c agree with f(x), Pn(c) = f(c), Pn'(c) = f'(c),.... Pn(n)(c) = f(n)(c). The difference between f(x) and the nth Taylor polynomial is called the nth Taylor remainder, Rn(x) = f(x) - Pn(x). Thus f(x) = f(c) + f'(c)(x - c) +
|
|||||||
Home  Infinite Series Infinite Series  Taylor's Formula Taylor's Formula  Taylor polynomials Taylor polynomials |
|||||||
Last Update: 2006-11-08



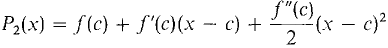

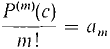


 (x - c)2 + ... +
(x - c)2 + ... +  (x - c)n + Rn(x).
(x - c)n + Rn(x).