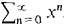| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Derivatives and Integrals of Power Series Derivatives and Integrals of Power Series  Problems Problems |
|






|
|
Problems
In Problems 1-10 find power series for f'(x) and for ∫0xf(t) dt.
In Problems 11-34 find a power series for the given function and determine its radius of convergence.
35 Check the formulas d(sinh x)/dx = cosh x, d(cosh x)/dx = sinh x by differentiating the power series. 36 Prove that if the power series
has radius of convergence r/b (b > 0). 37 Prove that if
has radius of convergence √r. 38 Prove that if
have radii of convergence r and s respectively and r ≤ s, then f(x) + g(x) has a radius of convergence of at least r. 39 Show that if
has radius of convergence r. 40 Evaluate 41 Evaluate
|
|
Home  Infinite Series Infinite Series  Derivatives and Integrals of Power Series Derivatives and Integrals of Power Series  Problems Problems |
|
Last Update: 2006-11-25






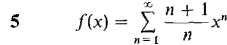





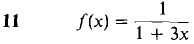







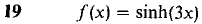









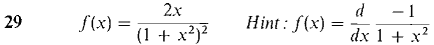





 has finite radius of convergence r, then the power series
has finite radius of convergence r, then the power series
 has finite radius of convergence r, then
has finite radius of convergence r, then

 has radius of convergence r, then for any positive integer p,
has radius of convergence r, then for any positive integer p,
 , using the derivative of the power series
, using the derivative of the power series 
 , using the first and second derivatives of
, using the first and second derivatives of