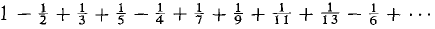Theorem 2

Given a series

one can form a new series by listing the terms in a different order, for example

a₁ + a₃ + a₂ + a₅ + a₄ + ....

Such a series is called a rearrangement of . The difference between absolute convergence and conditional convergence is shown emphatically by the following pair of theorems.

We shall not prove these theorems. Instead we give a pair of rearrangements of the conditionally convergent series

one diverging to ∞ and the other converging to - 1. The alternating series

conditionally converges to a number between ½ and 1.

To get a rearrangement which diverges to ∞, we write down terms in the following order:

• 1st positive term,
• 1st negative term,
• next 2 positive terms,
• 2nd negative term,
• next 4 positive terms,
• 3rd negative term,
• next 2^m positive terms,
• mth negative term,

We thus obtain the series

Each block of 2^m positive terms adds up to at least ¼,

However, all the negative terms except -1/2 and -¼ have absolute value ≤ 1/6. Hence after the mth negative term the partial sum is more than

Therefore the partial sums, and hence the series, diverge to x.

To get a rearrangement which converges conditionally to -1 we proceed as follows:

Write down negative terms until the partial sum is below -1, then positive terms until the partial sum is above -1, then negative terms until the partial sum is below -1, and so on.

The mth time the partial sum goes above -1, it must be between -1 and - 1 + (1/m). The with time it goes below -1 it must be between -1 and -1 -(1/m). Therefore the series converges to -1.