| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Absolute and Conditional Convergence Absolute and Conditional Convergence  Absolute And Conditional Convergence - Definition Absolute And Conditional Convergence - Definition |
|






|
|
Absolute And Conditional Convergence - Definition
9.6 ABSOLUTE AND CONDITIONAL CONVERGENCE Consider a series
which has both positive and negative terms. We may form a new series whose terms are the absolute values of the terms of the given series. If all the terms an are nonzero, then |an| > 0 so is a positive term series. If Sometimes it is simpler to study the convergence of the absolute value series DEFINITION A series
|
|
Home  Infinite Series Infinite Series  Absolute and Conditional Convergence Absolute and Conditional Convergence  Absolute And Conditional Convergence - Definition Absolute And Conditional Convergence - Definition |
|
Last Update: 2006-11-07



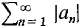

 is already a positive term series, then |an| = an and the series is identical to its absolute value series
is already a positive term series, then |an| = an and the series is identical to its absolute value series 
 than of the given series
than of the given series  . This is because we have at our disposal all the convergence tests for positive term series from the preceding sections.
. This is because we have at our disposal all the convergence tests for positive term series from the preceding sections. is said to be absolutely convergent if its absolute value series
is said to be absolutely convergent if its absolute value series  is convergent. A series which is convergent but not absolutely convergent is called conditionally convergent.
is convergent. A series which is convergent but not absolutely convergent is called conditionally convergent.