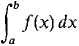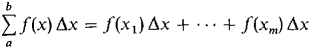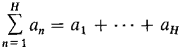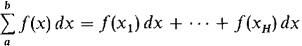| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Properties of Infinite Series Properties of Infinite Series  Partial Sum Σ Partial Sum Σ |
|||||||||||






|
|||||||||||
Partial Sum Σ
9.3 PROPERTIES OF INFINITE SERIES It is convenient to use capital sigmas, ∑, for partial sums and infinite series, as we did for finite and infinite Riemann sums. We write
for the mth partial sum,
for an infinite partial sum, and
for the infinite series. Thus S is the standard part of SH,
Sometimes we start counting from zero instead of one. For example, the formula for the sum of a geometric series can be written
Infinite series are similar to definite integrals. Table 9.3.1 compares and contrasts the two notions.
The difference between them is that the infinite series is formed by adding up the terms of an infinite sequence, while the definite integral is formed by adding up the values of f(x)dx for x between a and b. The definite integral of a continuous function always exists. But the problem of whether an improper integral converges is similar to the problem of whether an infinite series converges.
|
|||||||||||
Home  Infinite Series Infinite Series  Properties of Infinite Series Properties of Infinite Series  Partial Sum Σ Partial Sum Σ |
|||||||||||
Last Update: 2006-11-16


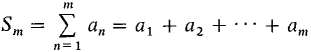

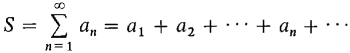
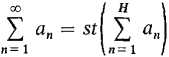
 , where |c| < 1.
, where |c| < 1.