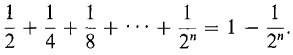| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Series Series  Series Series |
|






|
|
Series
9.2 SERIES The sum of finitely many real numbers a1, a2, ..., an is again a real number a1 + a2 + ... + an. Sometimes we wish to form the sum of an infinite sequence of real numbers, a1 + a2 + ... + an + .... For example, if a man walks halfway across a room of unit width, then half of the remaining distance, then half the remaining distance again, and so forth, the total distance he will travel is an infinite sum
In n steps he will travel
Thus he will get closer and closer to the other side of the room, and we have the limit
It is natural to call this limit the infinite sum,
We can go from this example to the general notion of an infinite sum. When we wish to find the sum of an infinite sequence <an> we call it an infinite series and write it in the form a1 + a2 + ... + an + ... Given an infinite sequence <an>, each finite sum a1 + ... + an is defined. This sum is called the nth partial sum of the series. Thus, with each infinite series a1 + a2 + ... + an+..., there are associated two sequences, the sequence of terms, a1, a2, ..., an,..., and the sequence of partial sums, S1, S2, ..., Sn, ... where Sn = a1 + ... + an. For each positive hyperreal number H, the infinite partial sum SH = a1 + ... + aH is also defined, by the Extension Principle.
|
|
Home  Infinite Series Infinite Series  Series Series  Series Series |
|
Last Update: 2006-11-07



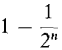 units,
units,