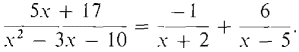The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Exponential and Logartihmic Functions Integration of Rational Functions Method For Integrating A Rational Function
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Method For Integrating A Rational Function

In all four examples the idea was to break the rational function into a sum of simpler functions which can easily be integrated. Here are three steps in the method.

METHOD FOR INTEGRATING A RATIONAL FUNCTION

08_exp-log_functions-459.gif

Step 1

If the degree of F(x) is ≥ the degree of G(x) apply long division. This puts the quotient F(x)/G(x) in the form

08_exp-log_functions-460.gif

where the degree of the polynomial R(x) is less than that of G(x).

Step 2

Break the quotient R(x)/G(x) into a sum of partial fractions.

Step 3

Integrate the polynomial Q(x) and each of the partial fractions separately. Sometimes Step 1 or 2 will be unnecessary.

We first factor the denominator a2 - 3x - 10. Since it has degree two we can find its roots from the quadratic formula.

08_exp-log_functions-461.gif

x = 5 and x = - 2.

By the Factor Theorem, x2 - 3x - 10 has the two factors x - 5 and x + 2, whence

a2 - 3a - 10 = (a + 2)(a - 5). Now we find the sum of partial fractions. It must have the form

08_exp-log_functions-462.gif

The way we find A and B is to use (x + 2)(x - 5) as a common denominator so the numerators of both sides of the equation are equal.

08_exp-log_functions-463.gif

The x terms and the constant terms must be equal, so we get two equations in the unknowns A and B.

5 = A + B, 17 = -5/1 + IB. Solving for A and B we have

A = -1, 5 = 6,

08_exp-log_functions-464.gif

Example 3 (Continued)
Example 4 (Continued)

EXAMPLE 4 is an integral of the form

08_exp-log_functions-480.gif

and was worked out in this way.
Home Exponential and Logartihmic Functions Integration of Rational Functions Method For Integrating A Rational Function

Last Update: 2006-11-05