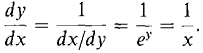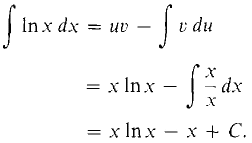| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Exponential and Logartihmic Functions Natural Logarithms Theorems |
|
 Search the VIAS Library | Index
|
  |
Theorems
Recall the Power Rule for integrals,
It shows how to integrate xn for n ≠ -1. Now, at long last, we are about to determine the integral of x-1. It turns out to be the natural logarithm of x. THEOREM 1 (i) On the interval (0, ∞),
(ii) On both the intervals (- ∞, 0) and (0, ∞),
PROOF (i) Let y = ln x. Then x = ey, dx/dy = ey. By the Inverse Function Theorem,
(ii) Let x < 0 and let y = ln|x|. For x < 0, |x| = -x so
Then
In the above theorem we had to be careful because 1/x is defined for all x ≠ 0 but lnx is only defined for x > 0. Thus on the negative interval (-∞, 0) the anti-derivative of 1/x cannot be lnx. Since |x| > 0 for both positive and negative x, ln|x| is defined for all x ≠ 0. Fortunately, it turns out to be the antiderivative of 1/x in all
Figure 8.5.1 cases. For x > 0, 1/x > 0 and ln|x| is increasing, while for x < 0, 1/x < 0 and ln |x| is decreasing (see Figure 8.5.1). We now evaluate the integral of ln x. This integral can be found in the table at the end of the book. THEOREM 2
PROOF We use integration by parts. Let
Then
|
|
| Home Exponential and Logartihmic Functions Natural Logarithms Theorems |
|
Last Update: 2006-11-16