| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Trigonometric Functions Trigonometric Functions  Area in Polar Coordinates Area in Polar Coordinates  Examples Examples  Example 2: Area of a Circle in Polar Coordinates Example 2: Area of a Circle in Polar Coordinates |
|






|
|
Example 2: Area of a Circle in Polar Coordinates
Find the area of the region inside the circle r = sin θ (Figure 7.9.7).
Figure 7.9.7 The point (r, θ) goes around the circle once when 0 ≤ θ ≤ π with r positive, and again when π ≤ θ ≤ 2π with r negative. The theorem says that we will get the correct area if we take either 0 and π, or π and 2π, as the limits of integration. Thus A = Alternatively, A = Since the curve is a circle of radius ½, our answer π/4 agrees with the usual formula A = πr2. Integrating from 0 to 2π would count the area twice and give the wrong answer.
|
|
Home  Trigonometric Functions Trigonometric Functions  Area in Polar Coordinates Area in Polar Coordinates  Examples Examples  Example 2: Area of a Circle in Polar Coordinates Example 2: Area of a Circle in Polar Coordinates |
|
Last Update: 2006-11-15



 = ¼(π - 0) = π/4.
= ¼(π - 0) = π/4.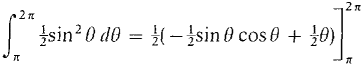 = ¼(2π - 7t) = π/4.
= ¼(2π - 7t) = π/4.