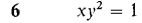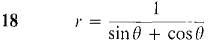Problems

1           Plot the following points in polar coordinates:

In Problems 2-12, find an equation in polar coordinates which has the same graph as the given equation in rectangular coordinates.

In Problems 13-20, sketch the given curve in polar coordinates.

In Problems 21-24, find rectangular parametric equations for the given curves.

25            Prove that if f(θ) = f(-θ) then the curve r = f(θ) is symmetric about the x-axis. That is, if (x, y) is on the curve then so is (x, -y).

26             Prove that if f(θ) = f(π + θ) then the curve r = f(θ) is symmetric about the origin. That is, if (x, y) is on the curve so is (-x, -r).

27             Prove that if f(θ) = f(π - θ) then the curve r = f(θ) is symmetric about the y-axis.