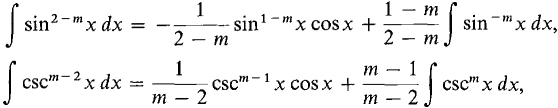| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Trigonometric Functions Trigonometric Functions  Integrals of Powers of Trigonometric Functions Integrals of Powers of Trigonometric Functions  Reduction Formulas (Secant and Cosecant) Reduction Formulas (Secant and Cosecant) |
|






|
|
Reduction Formulas (Secant and Cosecant)
THEOREM 3 Let m ≠ 1. Then (i)
(ii)
PROOF (ii) This can be done by integration by parts, but it is easier to use Theorem 2. Let n = 2 - m. For m ≠ 2, n ≠ 0 and Theorem 2 gives
whence
For m = 2 the formula is already known,
These reduction formulas can be used to integrate any even power of sec x or csc x, and to get the integral of any odd power of sec x or csc x in terms of ∫ sec x or ∫ csc x. We shall find ∫ sec x and ∫ csc x in the next chapter.
|
|
Home  Trigonometric Functions Trigonometric Functions  Integrals of Powers of Trigonometric Functions Integrals of Powers of Trigonometric Functions  Reduction Formulas (Secant and Cosecant) Reduction Formulas (Secant and Cosecant) |
|
Last Update: 2006-11-05