| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Trigonometric Functions Derivatives of Trigonometric Functions Theorem 2: Differentiability of Cosine and Sine |
|
 Search the VIAS Library | Index
|
  |
Theorem 2: Differentiability of Cosine and Sine
THEOREM 2 The functions x = cos θ and y = sin θ are differentiable for all θ, and d(sin θ) = cos θ dθ, d(cos θ) = - sin θ dθ.
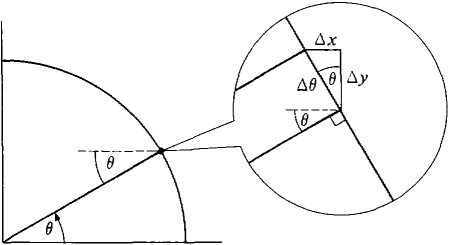
Figure 7.2.2 Discussion Intuitively, the small triangle in Figure 7.2.2 is infinitely close to a right triangle with angle θ and hypotenuse Δθ, whence
Notice that Δx is negative while Δy is positive when θ is in the first quadrant. The proof of Theorem 2 uses a lemma. LEMMA (i)
(ii)
PROOF (i) We show that for any nonzero infinitesimal Δθ,
When Δθ is positive we draw the figure shown in Figure 7.2.3. We have Area of triangle QOR < area of sector QOR < area of triangle QOS, ½ sin Δθ < ½Δθ < ½ tan Δθ. Then cos Δθ < Since cos θ is continuous, cos Δθ ≈ 1, whence
Figure 7.2.3 (ii) We compute the standard part of (cos Δθ - 1)/Δθ.
PROOF OF THEOREM 2 Let Δθ be a nonzero infinitesimal. Then
Here is a second proof that the derivative of the sine is the cosine. It uses the formula for the length of a curve in Section 6.3. ALTERNATE PROOF OF THEOREM 2 (Optional) Let 0 < θ < π/2 and x = cos θ, y = sin θ. Then (x, y) is a point on the unit circle as shown in Figure 7.2.4.
Figure 7.2.4 Take y as the independent variable. Then
θ is the length of the arc from 0 to y, so
By the Second Fundamental Theorem of Calculus,
Then by the Chain Rule.
and
Substituting cos θ for x and sin θ for y,
We can now find the derivatives of all the trigonometric functions by using the Quotient Rule
|
|
| Home Trigonometric Functions Derivatives of Trigonometric Functions Theorem 2: Differentiability of Cosine and Sine |
|
. 
, 
< 1.
≈ 1. 
Last Update: 2010-11-25