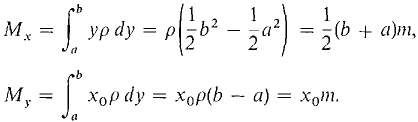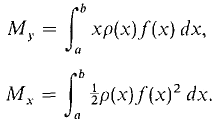Moments - Two Dimensions

Figure 6.6.8

A mass m at the point (x₀, y₀) in the (x, y) plane will have moments M_x about the x-axis and M_y about the y-axis (Figure 6.6.8). They are defined by

M_x = my₀,       M_y = mx₀.

Consider a vertical length of wire of mass m and constant density which lies on the line x = x₀ from y = a to y = b. The wire has density

The infinitesimal piece of the wire from y to y + Δy shown in Figure 6.6.9 will have mass and moments

Δm = ρ Δy,

ΔM_X ≈ y Δm = yρ Δy (compared to Δy),

ΔM_y ≈ x₀ Δm = x_oρΔy (compared to Δy).

 Figure 6.6.9

The Infinite Sum Theorem gives the moments for the whole wire,

We next take up the case of a flat plate which occupies the region R under the curve y = f(x), f(x) ≥ 0, from x = a to x = b (Figure 6.6.10). Assume the density

Figure 6.6.10

ρ(x) depends only on the x-coordinate. A vertical slice of infinitesimal width Δx between x and x + Δx is almost a vertical length of wire between 0 and f(x) which has area ΔA and mass Δm ≈ ρ(x) ΔA ≈ ρ(x) f(x) Δx (compared to Δx). Putting the mass Δm into the vertical wire formulas, the moments are

ΔM_y ≈ x Δm ≈ xρ(x) f(x) Δx              (compared to Δx),

ΔM_x ≈ ½(f(x) + 0) Δm ≈ ½ρ(x)f(x)²          Δx (compared to Δx).

Then by the Infinite Sum Theorem, the total moments are

The center of mass of a two-dimensional object is defined as the point (x, y) with coordinates

x = M_y/m,       y = M_x/m.

A single mass m at the point (x, y) will have the same moments as the two-dimensional body, M_x = my, M_y, = mx. The object will balance on a pin placed at the center of mass.

If a two-dimensional object has constant density, the center of mass depends only on the region R which it occupies. The centroid of a region R is defined as the center of mass of an object of constant density which occupies R. Thus if R is the region below the continuous curve y = f(x) from x = a to x = b, then the centroid has coordinates

where A is the area

Example 4

The following principle often simplifies a problem in moments.

If an object is symmetrical about an axis, then its moment about that axis is zero and its center of mass lies on the axis.

Figure 6.6.12 Symmetry about the y-axis

Example 5