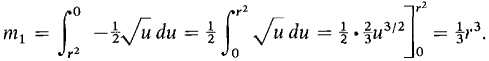| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Applications of the Integral Applications of the Integral  Some Applications to Physics Some Applications to Physics  Examples Examples  Example 2 Example 2 |
|






|
|
Example 2
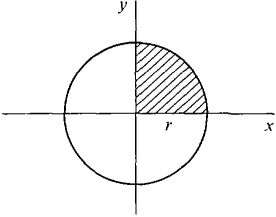
A circular disc of radius r has density at each point equal to the distance of the point from the y-axis. Find its mass. (The center of the circle, shown in Figure 6.6.4, is at the origin.) The circle is the region between the curves -
Put u = r2 - x2, du = -2xdx; u = r2 when x = 0, and u = 0 when x = r.
Then m = 4m1 = (4/3)r3.
Figure 6.6.4
|
|
Home  Applications of the Integral Applications of the Integral  Some Applications to Physics Some Applications to Physics  Examples Examples  Example 2 Example 2 |
|
Last Update: 2006-11-15


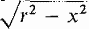 and
and 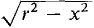 from -r to r. The density at a point (x, y) in the disc is |x|. By symmetry, all four quadrants have the same mass. We shall find the mass m1 of the first quadrant and multiply by four.
from -r to r. The density at a point (x, y) in the disc is |x|. By symmetry, all four quadrants have the same mass. We shall find the mass m1 of the first quadrant and multiply by four.