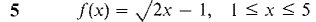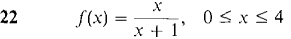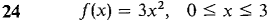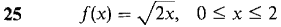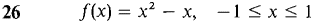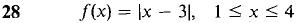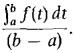Problems

In Problems 1-8, sketch the curve, find the average value of the function, and sketch the rectangle which has the same area as the region under the curve.

In Problems 9-22, find the average value of/(x).

In Problems 23-28, find a point c in the given interval such that f(c) is equal to the average value of f(x).

29            What is the average distance between a point x in the interval [5, 8] and the origin?

30            What is the average distance between a point in the interval [-4, 3] and the origin?

31            Find the average distance from the origin to a point on the curve y = x^3/2, 0 ≤ x ≤ 3, with respect to x.

32            A particle moves with velocity v = 6t from time t = 0 to t = 10. Find its average velocity with respect to (a) time, (b) distance.

33            An object moves with velocity v = t³ from time t = 0 to t = 2. Find its average velocity with respect to (a) time, (b) distance.

34            A particle moves with positive velocity v = f(t) from t = a to t = b. Thus its average velocity with respect to time is

Show that its average velocity with respect to distance is